Why Do Students Find Limit Calculation Difficult?
The purpose of algebra is to understand the symbols and then extract the answers from the equations. Most students, however, are unable to grasp this concept, which is why they have difficulties doing calculations. It is difficult for pupils to arrive at the correct solution when they have inadequate conceptualizations and fundamentals.
But don’t worry, since the limit calculator has eradicated all of the obstacles that academics have when solving mathematical problems.
This free limit solver can help you enumerate immediate results for limit issues, as the name implies. Students are uninterested in limits and arithmetic analysis since it is a difficult task. That is why our free tool rushes in to assist you immediately away. What do you think?
Anyway, let us now turn our attention to the pivot. Do you wish to look at the flaws that prevent pupils from learning about limit computations? If that’s the case, read on for more information.
Continue on!
Limits – Is That Something Horrible?
Students may find it difficult to implement the limit strategy at times. For all who are unsure what to do, there are four approaches for solving the restriction. Calculator-limit online.net’s calculator can assist you in determining which method to choose. When looking for the roots of a limit, you can utilize the factoring method.
Another problem is that children can’t tell the difference between rational and convoluted numbers. It becomes a significant issue for students when they are unable to devise a strategy to implement in their heads. The main reason for this is that the students are unclear about which method to take.
The limit calculator with steps helps students figure out what kind of number they’re working with and if they can get information about the number’s validity quickly. They’ll be able to deal with a specific problem and determine what kind of number they’re dealing with. If you utilize the limit evaluator and get an undefined number in the denominator, you can’t use the replacement strategy. Limit calculators can help us figure out which method to utilize, such as substitution, factoring, rationalizing, or the Least Common Multiple Methods.
The Factoring Technique:
The Limit solver can help you decide whether or not to apply the factoring technique. If we already know the function’s roots, we’ll use the factoring approach.
There are various reasons to employ the factoring approach in order to follow the factoring method’s solution:
F(x)= x4x2-6x+9x-3,
F(x)= x4x2-6x+9x-3,
F(x)= x F(x)= x3x2-12x+36x-6,
F(x)= x3x2-12x+36x-6,
F(x)= x F(x)= x2x2-8x+16x-4,
F(x)= x2x2-8x+16x-4, F(x)= x
Take into account all of the functions; they can all be taken into account.
x2-6x+9= (x-3) (x-3)
x2-12x+36= (x-6) (x-6)
(x-4) = x2-8x+16 (x-4)
All rationalized roots functions and denominator-cut functions. To begin, we’ll seek these functions that have roots in the Limits calculator, and then we’ll utilize factoring to solve the limit.
The Rationalizing Strategy:
The rationalizing strategy is used when both factoring and substitution approaches fail to solve the limit.
Think about the following function:
F(x)=x14x-7 -3x-14
F(x)=x14x-7 -3x-14 F(x)=x14
The function is incomprehensible when we implement the limit. As we can see from the fact that the denominator is ‘0,’ the Limit calculator makes the limit evaluator straightforward for us. It would make the limit as a whole unsolvable.
To find the counterpart of the x-7 -3x-11.x-7+3x-7+3, we’ll mix both the denominator and the numerator. As a consequence, students will be able to identify the limit.
Multiplying with the conjugate of the function makes the question considerably easy for the students.
The Replacement Approach:
In this part, we’ll go through a few examples to show you how to utilize the replacement approach to solve issues with constraints. This approach is also employed by a free online limit calculator. The replacement strategy should be utilized if the limit evaluator is still solvable. Examine the following function while applying the limit:
F(x)= x8x2-9x+18x-7
F(x)= x8x2-9x+18x-7 F(x)= x
We’ll use the replacement strategy to apply the limit evaluator in the preceding function because the limit is still solvable.
Now have a look at a function like the one below:
F(x)= x4x2-9x+5x-4
F(x)= x4x2-9x+5x-4 F(x)= x
The denominator will become undefined when we construct the limit evaluator, which in this case is x4, and when we insert the limit evaluator in the function, the denominator will become ‘0’. The Limit calculator can help here since it allows us to examine whether or not a function is defined before setting a limit. The outcome of partitioning the numerator by the polynomial is an indeterminate function. We’ll take a different strategy in this circumstance.
Why Should You Use a Limit Calculator?
You may use the Limit calculator to get the upper and lower limit evaluator of variables. The limit finder, on the other hand, can assist you in identifying constraints by completing the instructions below
- Start by entering the equations or functions.
- From the drop-down menu, select the variable for which you want to establish a limit. Any of the following might be it: x, y, z, a, b, c, or n.
- Set the threshold at which the limit will be determined. In this area, you may alternatively use a simple word like “inf=” or “pi =”.
- Now is the time to choose the limit’s orientation. It has the potential to be both beneficial and destructive.
- Once you’ve entered the values in the fields, the calculator will display an equation preview.
- Just use the calculate button to do a calculation.
Last But Not Least:
We examined why limitations are a difficult strategy for kids to embrace in this guidepost. In addition, the usage of a limit calculator has been highlighted in the context in order to lessen the difficulties associated with this algebraic method. We hope that this article will prove to be a useful resource for students.
Additional Resources:
The importance of methodology to make learning mathematics easier.
Limits in differential calculus linking to derivatives.


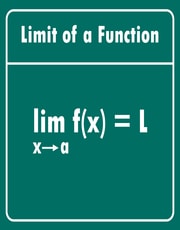

 Coding involves the implementation of an algorithm into a code. It can get done with the help of a programming language. Thus, the system and process work using an appropriate syntax. It depends on the chosen
Coding involves the implementation of an algorithm into a code. It can get done with the help of a programming language. Thus, the system and process work using an appropriate syntax. It depends on the chosen 


 Katie Brenneman is a passionate writer specializing in education, mental health, family lifestyle and online safety. When she isn’t writing, you can find her with her nose buried in a book or hiking with her dog, Charlie. You can follow her on
Katie Brenneman is a passionate writer specializing in education, mental health, family lifestyle and online safety. When she isn’t writing, you can find her with her nose buried in a book or hiking with her dog, Charlie. You can follow her on 

